Plano inclinado con dos masas
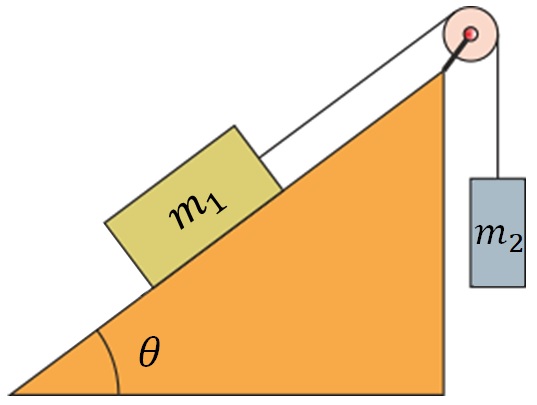
Dos masas unidas por una cuerda ligera se colocan en un plano inclinado con una polea. La masa m_{1} se ubica sobre la superficie inclinada del plano, mientras que la masa m_{2} cuelga desde la polea, como en la figura. Si la tensión sobre la cuerda es uniforme y no hay fricción, ¿en qué dirección se moverá el sistema?
Primero busquemos la condición para que el sistema se encuentre en equilibrio, es decir:
a=0
La tensión que ejerce el cable para sostener a la masa que cuelga es igual al peso de ésta, es decir:
T=m_{2}g
La tensión que ejerce el cable para sostener a la masa que está en la superficie inclinada es igual al peso de ésta multiplicada por el seno del ángulo de inclinación:
T=m_{1}gsen\theta
Puesto que la tensión es uniforme, podemos igualar las dos ecuaciones. Al cancelar la gravedad en ambos lados, obtenemos la condición de equilibrio:
m_{2}=m_{1}sen\theta
En el caso particular donde \theta=30° la tensión que sostiene la masa 1, que descansa sobre el plano, se reduce a la mitad, ya que sen(30°)=\frac{1}{2} . Entonces, basta con que la masa 2 sea la mitad de la masa 1 para que el sistema permanezca en equilibrio en este caso.
Para que el sistema se mueva en la dirección por la que cae la masa 2, la condición es que:
m_{2}>m_{1}sen\theta
Para que el sistema se mueva en la dirección por la que se desliza la masa 1 sobre el plano, entonces:
m_{2}<m_{1}sen\theta

